Chapter I: Basics
1 Introduction
Although computer graphics is a vast field that encompasses almost any graphical aspect, we are mainly interested in the generation of images of 3-dimensional scenes. Computer imagery has applications for film special effects, simulation and training, games, medical imagery, flying logos, etc.
Computer graphics relies on an internal model of the scene, that is, a mathematical representation suitable for graphical computations (see Chapter II). The model describes the 3D shapes, layout and materials of the scene.
This 3D representation then has to be projected to compute a 2D image from a given viewpoint, this is the rendering step (see C hapter III). Rendering involves projecting the objects (perspective), handling visibility (which parts of objects are hidden) and computing their appearance and lighting interactions. Finally, for animated sequence, the motion of objects has to be specified. We will not discuss animation in this document.
2 Pixels
A computer image is usually represented as a discrete grid of picture elements a.k.a. pixels. The number of pixels determines the resolution of the image. Typical resolutions range from 320*200 to 2000*1500. For a black and white image, a number describes the intensity of each pixel. It can be expressed etween 0.0 (black) and 1.0 (white). However, for internal binary representation reasons, it is usually stored as an integer between 0 (black) and 255 (white)
A low-resolution digital image. Left: Black and white. Right: Color. (Image © Pixar).
For a color image, each pixel is described by a triple of numbers representing the intensity of red, green and blue. For example, pure red is (255, 0, 0) and purple is (255, 0, 255).
Because the image is represented by a discrete array of pixels, aliasing problems may occur. The most classical form of aliasing is the jaggy aspect of lines (see figure below). Antialiasing techniques are thus required. In the case of the line, it consists in using intermediate gray levels to “smooth” the appearance of the line. Another form of aliasing can be observed on television when people wear shirts with a fine stripped texture. A flickering pattern is observed because the size of the pattern is on the same order of magnitude as the pixel size.
Chapter II: Geometric Model
We introduce how the geometry of the scene is represented in the memory of the computer.
1 Polygons
The most classical method for modeling 3D geometry is the use of polygons. An object is approximated by a polygonal mesh, that is a set of connected polygons (see below). Most of the time, triangles are used for simplicity and generality.
Left: A cow modeled as a mesh of triangles.
Right: This triangle can be stored using the coordinates of its vertices as [(2,4,2), (3,1,0), (1,1,2)].
Each polygon or triangle can be described by the 3D coordinates of its list of vertices (see figure above). The obvious limitation of triangles is that they produce a flat and geometric appearance. However, techniques called smoothing or interpolation can greatly improve this.
2 Primitives
The most classical geometric entities can be directly used as primitives, e.g. cubes, cylinders, spheres and cones. A sphere for example can be simply described by the coordinates of its center and its radius.
3 Smooth patches
More complex mathematical entities permit the representation of complex smooth objects. Spline patches and NURBS are the most popular. They are however harder to manipulate since one does not directly control the surface but so called control points that are only indirectly related to the final hape. Moreover, obtaining smooth junctions between different patches can be problematic. However, the recently popular subdivision surfaces overcome this limitation. They offer the best of both worlds and provide the simplicity of polygons and the smoothness of patches.
Chapter III: Rendering
1 Projection and rasterization
The image projection of the 3D objects is computed using linear perspective. Given the position of the viewpoint and some camera parameters (e.g. field of view), it is very easy to compute the projection of a 3D point onto the 2D image. For mathematics enthusiasts, this can be simply expressed using a 4*4 matrix.
In most methods, the geometric entities are then rasterized. It consists in drawing all the pixels covered by the entity.
In the example below, the projections of the 3 red points have been computed using linear perspective, and the triangle has then been rasterized by filling the pixels in black. For richer rendering, the color of each rasterized pixel must take into account the optical properties of the object, as we will discuss below.
Projection (left) and rasterization (right) of a triangle.
2 Visibility
If the scene contains more than one object, occlusions may occur. That is, some objects may be hidden by others. Only visible objects should be represented. Visibility techniques deal with this issue.
One classical algorithm that solves the visibility problem is the so-called painter’s algorithm. It consists in sorting the objects or polygons from back to front and rasterizing them in this order. This way, front-most polygons cover the more distant polygons that they hide.
The Painter’s algorithm. Triangle 1 is drawn first because it is more distant. Triangle 2 is drawn next and
covers Triangle 1, which yields correct occlusion.
The ray-tracing algorithm does not use a rasterization phase. It sends one ray from the eye and through each pixel of the image. The intersection between this ray and the objects of the scene is computed, and only the closest intersection is considered.
Ray-tracing. A ray is sent from the eye and through the pixel. Since the intersection with 2 is closer than
the intersection with 1, the pixel is black.
The z-buffer method is the most common nowadays (e.g. for computer graphics cards). It stores the depth (z) of each pixel. When a new polygon is rasterized, for each pixel, the algorithm compares the depth of the current polygon and the depth of the pixel. If the new polygon has a closer depth, the color and depth of the pixel are updated. Otherwise, it means that for this pixel, a formerly drawn polygon hides the current polygon.
3 Shading and materials
Augmenting the scene with light sources allows for better rendering. The objects can be shaded according to their interaction with light. Various shading models have been proposed in the literature. They describe how light is reflected by object, depending on the relative orientation of the surface, light source and viewpoint (see figure below).
Light reflection model. The ratio of light bouncing off the surface in the direction of the eye depends on the two angles.
Sphere rendered using various material models. Note in particular the different highlights. Image from the Columbia-Utrecht Reflectance and Texture Database.
Texture mapping uses 2D images that are mapped on the 3D models to improve their appearance (see examples in section 5).
4 Shadows and lighting simulation
Shading and material models only take into account the local interaction of surfaces and light. They doe not simulate shadows that are harder to handle because they imply long-range interactions. A shadow is caused by the occlusion of light by one object.
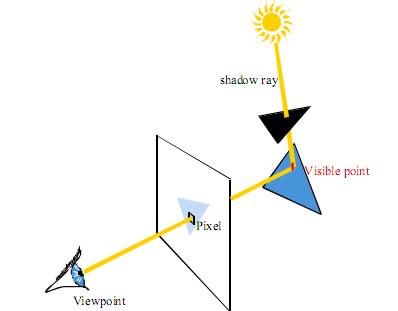
Ray-tracing, for example, can handle shadows, but requires a shadow computation for each pixel and each light source. A shadow ray is sent from the visible point to the light source. If the ray intersects an object, then the visible point is in shadow.
Shadow computation using ray-tracing. The visible point is in shadow because the black triangle occludes the light source.
More complex lighting interactions can then be simulated. In particular, objects that are illuminated by a primary light source reflect light and produce indirect lighting. This is particularly important for inddor scenes. Global lighting methods take into account all light inter-reflections within the scene.
5 Example